7. Construir un diagrama de flujo para explicar como resolver integrales directas o primitivas y desarrollar por lo menos diez ejercicios diferentes.


1.    Construir un diagrama de flujo para explicar como resolver integrales directas o primitivas y desarrollar por lo menos diez ejercicios diferentes.

Uno de los problemas fundamentales que se plantea el Cálculo de una variable geométricamente es el cálculo del área que encierra el gráfico de una función definida en un intervalo [a, b] con el eje de abscisas (y = 0).
Dicha área se puede obtener con la integral definida. En Economía la integral definida aparece ante problemas de determinación de funciones totales a partir de funciones marginales (utilidad marginal ⇒ utilidad total) o, bien, ante procesos que terminan en una “suma” en variables continua como es el caso del cálculo de funciones financieras de capitalización partiendo del concepto de tanto instantáneo de interés.

Son frecuentes las técnicas de la integral en muchos análisis estadísticos de ciertos fenómenos de la realidad económica y empresarial (teoría de las probabilidades, matemática actuarial, etc.)

Para resolver integrales definidas es necesario conocer previamente los distintos métodos de cálculo de primitivas que también es conocida como la “antiderivada” de una función.

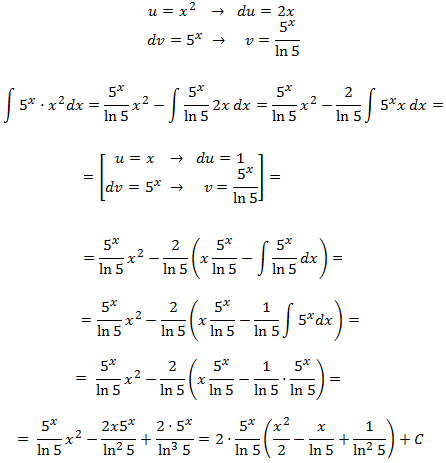
Resultado de imagen para Construir un diagrama de flujo para explicar como resolver integrales directas o primitivas y desarrollar por lo menos diez ejercicios diferentes.
https://www.uv.es/perezsa/docencia/material/IMEE/CalculoPrimitivas.pdf

Comentarios

Publicar un comentario

Entradas populares de este blog

3. Importancia que tiene el estudio del cálculo integral en la vida diaria, mencionando y explicando en al menos tres ejemplos en los que se vea reflejado su explicación.

Imagen
1.     Importancia que tiene el estudio del cálculo integral   en la vida diaria, mencionando y explicando en   al menos tres ejemplos en los que se vea reflejado su explicación. El estudio de las matemáticas es un factor muy importante para el desarrollo de la vida, ya que los cálculos matemáticos están presentes en cada momento de nuestra vida.  Esta ciencia se encuentra divida en varias ramas como lo es: la aritmética, el álgebra, la trigonometría, la geometría, el cálculo diferencial e integral, etc.   El cálculo integral, es el proceso de integración o anti derivación, es muy común en la ingeniería y en la matemática en general y se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.  En este proyecto se hablara de las aplicaciones del cálculo integral (integrales definidas). https://www.monografias.com/.../Aplicacion-de-integrales-en-la-vida-diaria-F3Z29R2J...
Leer más

4. Campos en los que se aplica el cálculo diferencial e integral, para cada caso describir en que consisten.

Imagen
1.     Campos en los que se aplica el cálculo diferencial e integral, para cada caso describir en que consisten. El álgebra y la trigonometría nos sirven para estudiar los objetos que se mueven velozmente a lo largo de una trayectoria rectilínea o circular, pero si la velocidad es variable o la trayectoria es irregular es necesario el cálculo. www.academico.cecyt7.ipn.mx/cal_int/menus/unidad2_calcint/unidad2_tema1.html
Leer más

9. Demostrar el concepto de los métodos de integración por: cambio de variable, sustitución, por partes a través de 5 ejercicios mínimo por cada método.

Imagen
1.     Demostrar el concepto de los métodos de integración por: cambio de variable, sustitución, por partes a través de 5 ejercicios mínimo por cada método. Integración por cambio de variable. Nos proporciona un proceso que permite reconocer cuándo un integrando es el resultado de una derivada en la que se ha usado la regla de la cadena. Sea f(x) la función que deseamos integrar, entonces hacemos el siguiente cambio de variable:  x = g(t), d(x) = g'(t)dt , con lo que: Integración por partes. Este método nos permitirá resolver integrales de funciones que pueden expresarse como un producto de una función por la derivada de otra. Sean  u  y  v  dos funciones continuas, derivables y sus derivadas du y dv son integrables, entonces: u=f(x), v=g(x) , luego  du=f'(x)dx, dv=g'(x)dx :  Integración de funciones racionales: Vamos a integrar funciones racionales (cociente de polinomios), que siguen la forma: En ...
Leer más